The Friedman Test
A statistical tool to compare repeated samples or measures when parametric assumptions aren't met
Complete the form below to unlock access to ALL audio articles.
There are many circumstances in which it is necessary to compare repeated measures or samples, such as following a person's biological functions over time or repeated measurements of a chemical's concentration in a cell culture. While the one-way analysis of variance (ANOVA) test may be used, not all datasets meet its parametric assumptions, and an alternative must be sought. In this article, we consider one such test, the Friedman test, its assumptions, when to use it and go through a worked example.
What is the Friedman test?
Friedman test formula
What are the assumptions of Friedman’s test?
When to use a Friedman test
Friedman test interpretation
Friedman test example
What is the Friedman test?
The Friedman test, also sometimes referred to as Friedman’s two-way analysis of variance by ranks, is a non-parametric statistical test used to investigate whether groups of three or more repeated measurements differ from each other. It is used when the data in the variable of interest are ordinal or continuous (see assumptions for more details). The test is non-parametric because it does not assume any distributions in the data (such as the Normal distribution). In practice, the Friedman test is often used when the continuous variable has violated the assumptions needed for the one-way ANOVA or when the variable of interest is ordinal.
Friedman test formula
To find the test statistic for the Friedman test, Friedman’s F, we use the following formula:
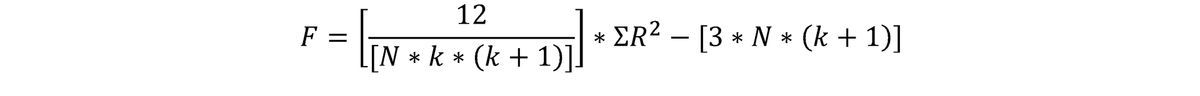
Where N is the number of individuals, k is the number of conditions (measurements or samples), and R is the total ranks for each of the columns of data. Further details are illustrated in the worked example.
What are the assumptions of Friedman’s test?
As with all statistical tests, the Friedman test has some assumptions, which are as follows:
- Data should be ordinal or continuous. An example of an ordinal variable is a survey question that ranks a five-point satisfaction scale from “most satisfied” to “least satisfied”. Examples of continuous variables are height, temperature and test performance (0 –100).
- Data must come from a single group measured at three or more different time points or related variables (see next section). Note that the Friedman test can technically be done on two or more samples/measurements, but then becomes identical to the Sign test. The Friedman test is therefore usually applied to three or more samples/measurements.
- The data should be a random sample from the population the investigator is aiming to make an inference about.
- Blocks of data must be mutually independent (the sets of data should not affect each other).
When to use a Friedman test
There are two distinct scenarios where the Friedman test might be useful:
- Where the same quantitative (continuous or ordinal) variable is measured two (more often three) or more times from the same sample at different time points (or from different samples that have been matched on another variable). For example, cholesterol measurements taken from the same group of patients in a study at three monthly intervals.
- Where two (more often three) or more related quantitative variables are measured from the same group at the same time. For example, responses to three related survey questions from the same group of individuals.
These scenarios are different in reality, but are actually variations on the same statistical question that can both be investigated under the same statistical test.
Friedman test interpretation
As with the one-way ANOVA, the results of the hypothesis test for Friedman’s test will give us a formal idea of whether the sets of values differ in some way, but does not tell you which one is different. This can normally be done by analyzing the median (a measure of central tendency) and interquartile range (IQR) (a measure of spread) of the multiple sets and judging whether there is some pattern of larger or smaller values among them.
Friedman test example
Suppose an investigator is interested in analyzing whether there is a difference in the pulmonary function test values of a group of 12 patients across 3 time points (Figure 1).

Figure 1: Test subjects awaiting a pulmonary function test. Credit: Technology Networks.
Step one is to present the null and alternative hypotheses.
- The null hypothesis (H0) is that all three blocks of pulmonary function test values are the same across the time points.
- The alternative hypothesis (H1) is that the blocks of pulmonary function test values are different in some way.
Step two is to sort the data into blocks or sets and rank them across rows.
The pulmonary function test values for all 12 patients at each of the 3 time points are given below, along with their ascending ranks across the rows (Table 1). For patient 1 for example, the rank for time 1 is 1 because this is the lowest value, time 3 is ranked 2 because it is next, and time 2 is 3 because it is highest.
Table 1: Pulmonary function test results for 12 patients at 3 time points, and their ranks in ascending order.
|
| Values | Ranks | ||||
| Patient | Time 1 | Time 2 | Time 3 | Time 1 | Time 2 | Time 3 |
| 1 | 15 | 19 | 17 | 1 | 3 | 2 |
| 2 | 15 | 33 | 23 | 1 | 3 | 2 |
| 3 | 44 | 15 | 9 | 3 | 2 | 1 |
| 4 | 6 | 17 | 20 | 1 | 2 | 3 |
| 5 | 12 | 34 | 33 | 1 | 3 | 2 |
| 6 | 14 | 18 | 17 | 1 | 3 | 2 |
| 7 | 35 | 24 | 20 | 3 | 2 | 1 |
| 8 | 36 | 32 | 17 | 3 | 2 | 1 |
| 9 | 36 | 26 | 34 | 3 | 1 | 2 |
| 10 | 23 | 12 | 9 | 3 | 2 | 1 |
| 11 | 7 | 9 | 18 | 1 | 2 | 3 |
| 12 | 9 | 10 | 4 | 2 | 3 | 1 |
By summing (adding together) the ranks at each time point:
R1 = 23
R2 = 28
R3 = 21
Given there are 12 patients (N = 12) and 3 time points (k = 3), we can calculate Friedman’s F as follows:
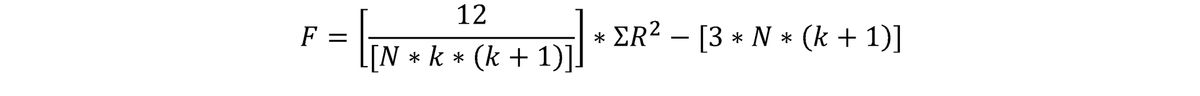
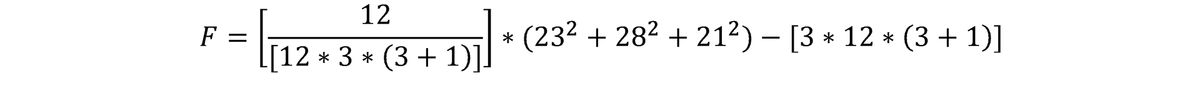
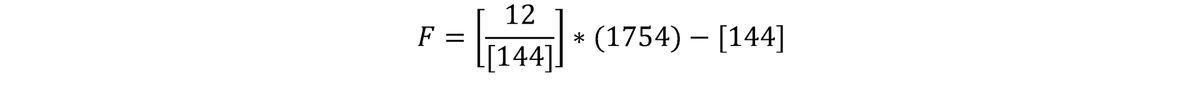
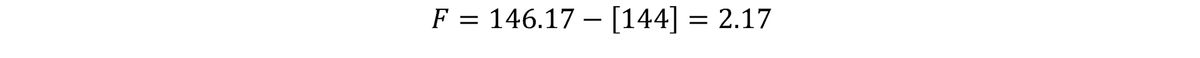
We find the test statistic to be F = 2.17.
Step four is to conduct a hypothesis test by finding the critical value of Friedman’s F.
There are two ways to conduct the hypothesis test for the Friedman test depending on the size of your sample and how many sets of data there are. One rule of thumb is that if you have k < 6 and N < 14, as in our example, you determine the critical value of F by looking at the table of critical values for Friedman’s test. Assuming we are interested in the α < 0.05 significance level (standard in statistical testing), the critical value corresponding to our k and N values is 6.17.
The alternative approach if you have k > 5 or N > 13, we determine our critical value by looking at the Chi-squared distribution values table using degrees of freedom (df) calculated by k – 1. The df is the quantity of the values included in a statistical test.
Under both approaches, we reject the null hypothesis if the calculated F value is larger than the critical value. Therefore, since in our example the F statistic 2.17 is smaller than the critical value 6.17, we do not reject the null hypothesis and conclude that there is no evidence for a difference between the pulmonary function test values across the three time points.
Further reading:
- UNL Department of Psychology. Friedman's two-way analysis of variance by ranks -- Analysis of k-within-group data with a quantitative response variable. University of Nebraska-Lincoln, Department of Psychology, https://psych.unl.edu/psycrs/handcomp/hcfried.PDF, Accessed 7 May 2024.
- Laerd Statistics. Friedman test in SPSS statistics. Laerd Statistics, https://statistics.laerd.com/spss-tutorials/friedman-test-using-spss-statistics.php, Accessed 7 May 2024.
- Laerd Statistics. Sign test using SPSS statistics. Laerd Statistics, https://statistics.laerd.com/spss-tutorials/sign-test-using-spss-statistics.php, Accessed 21 May 2024
- Jim Frost. Degrees of freedom in statistics. Statistics by Jim, https://statisticsbyjim.com/hypothesis-testing/degrees-freedom-statistics/, Accessed 8 May 2024.